Mathematical Implementation of RNN Encoder-Decoder for Neural Machine Translation
Technical deep dive into RNN encoder-decoder architecture for Neural Machine Translation with Word2Vec.
In the previous blog, we explored the precursor to modern attention mechanisms, Bahdanau Attention, which introduced a way for neural networks to softly search for relevant source words during translation. If you haven’t read that post yet, I encourage you to do so, as it provides helpful conceptual background for understanding the evolution of neural machine translation models.
In this blog, however, we shift our focus to the mathematical and technical implementation of the traditional RNN encoder-decoder architecture for language translation. Specifically, we will cover:
Vector representation of words using Word2Vec,
The workings of a Recurrent Neural Network (RNN), and,
The RNN encoder-decoder architecture for neural machine translation.
Vector Representation
Various implementations such as Bag of words have been used for representing words as vectors where, each vector ideally captures the meaning and, if possible, the semantics of a word in a given sentence. One of the most novel and widely adopted techniques for this purpose is Word2Vec.
While a detailed implementation of Word2Vec is beyond the scope of this blog, we will briefly cover the core concepts necessary to understand its role in Natural Language Translation. If you’re interested in a dedicated blog post on Word2Vec, let us know in the comments.
Word2Vec
Word2Vec is a neural network-based model trained on large corpora, commonly on datasets like Wikipedia. It uses a simple feedforward neural network where the input is a one-hot encoded vector representing a word, and the output is its corresponding dense vector in an n-dimensional embedding space.
You might be familiar with the classic analogy:
vector("King") − vector("Man") + vector("Woman") ≈ vector("Queen").
This illustrates how each word’s vector is positioned in the embedding space to reflect its meaning. Words with similar meanings are located closer together, while unrelated words are positioned farther apart. For Example;
distance(vector("fruit"), vector("apple")) is small, and,
distance(vector("fruit"), vector("car")) is large.
It's also important to note the presence of special tokens like <SoS> (Start-of-Sequence) and <EoS> (End-of-Sequence). These tokens mark the beginning and end of a sentence, respectively, and are crucial for translation tasks. Hint, they help the model understand where a sentence starts and ends, especially useful during decoding when the model needs to know when to stop generating words.
Architecture of Recurrent Neural Networks
Recurrent Neural Networks (RNNs) are a class of neural networks characterized by their use of loops to allow information to persist across time steps. In essence, RNNs maintain an internal state (or memory) that is updated as the network processes each element in a sequence.
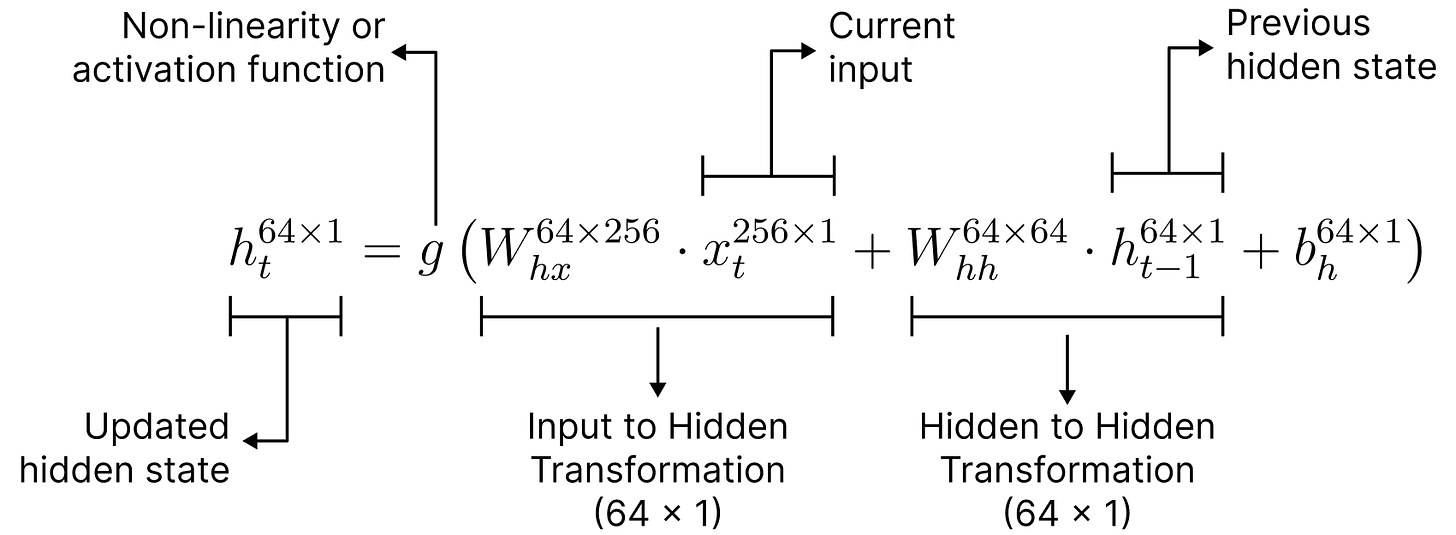
In our case, the input to the RNN is a sequence of word vectors (from Word2Vec). The time gap between two consecutive vectors is referred to as a time step. At each time step, the RNN maintains a fixed-size vector called the hidden state, which captures the context accumulated so far. This fixed size is commonly referred to as the hidden size of the RNN.
Updating the Hidden State
The hidden state acts as an internal memory for the RNN and evolves at each time step. This process is also known as unfolding the RNN through time.
The update mechanism involves two sets of weight matrices:
The updated hidden state at each step is calculated by summing the contribution from current input, previous hidden state, and bias term.
A detailed mathematical diagram is provided below. In our example, we assume:
Hidden size = 64
Word2Vec embedding dimension = 256
Where, g represents non-linearity or activation function like tanh or sigmoid.
This configuration is illustrative and can be adjusted based on specific tasks or model designs. The notations on superscript represents the dimension of vectors.
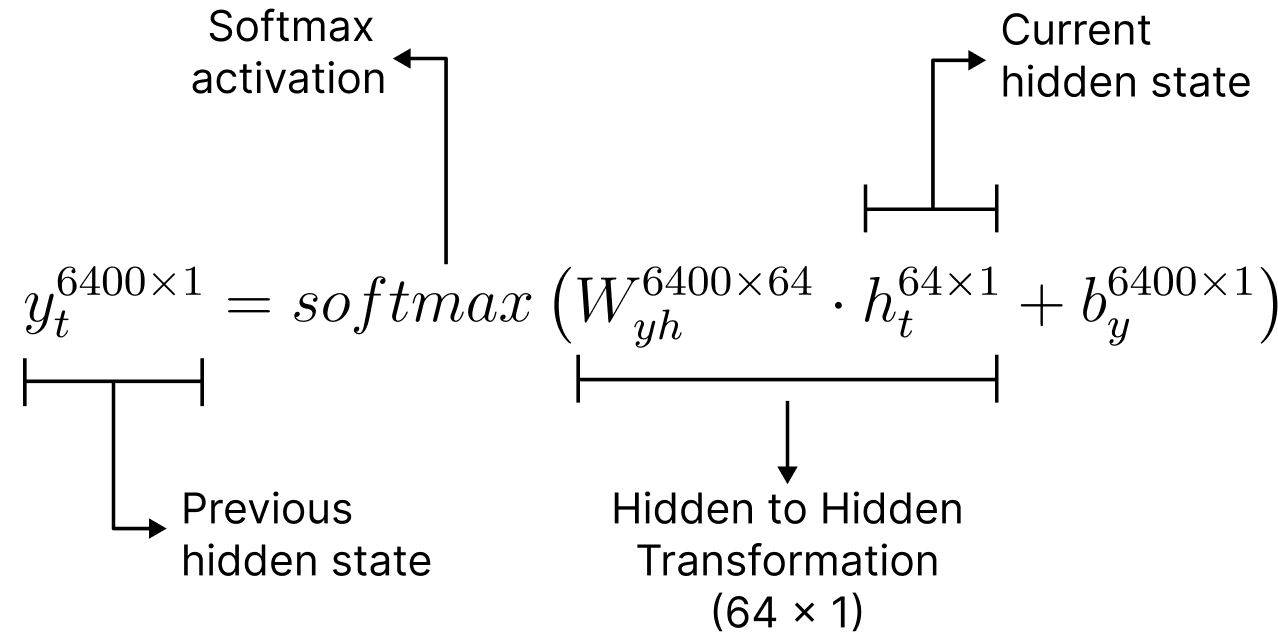
Computing the Output at each Timestep
At each timestep, the output of an RNN is computed using a feedforward (dense) layer that takes the current hidden state as input. This mechanism involves weight and bias matrices as follows:
The mathematical formula is given as;
The output dimension is determined by the number of neurons in this feedforward layer, which in turn defines the shape of the corresponding weight and bias matrices.
In our example, we assume an output size of 6400, meaning the final dense layer contains 6400 neurons—corresponding to a vocabulary size of 6400 words. And the softmaxed output represents the probability of occurrence of each word from the vocabulary.
Traditional RNN Encoder-Decoder for Translation
A traditional RNN-based translation model operates in two stages: encoding and decoding.
Encoding Stage
During encoding, the input sentence is passed through an encoder RNN that processes each word sequentially and generates a fixed-length context vector summarizing the entire sentence.
For example, consider the sentence:
“I love Apple”
This input is converted into a sequence of vectors: [x₁, x₂, x₃].
At the first timestep t=1, the hidden state is computed as:
Here, h0 is the initial hidden state, which is typically a zero vector of size equal to the RNN’s hidden dimension—indicating no prior context at t = 0.
This process is repeated for each timestep. By the final step t = 3, the encoder outputs the final hidden state h3, which serves as the context vector summarizing the input sentence.
Decoding Stage
The decoder RNN takes the final hidden state of the encoder as its initial hidden state:
At each subsequent timestep, the decoder updates its hidden state and produces an output vector. The output dimension is again 6400 × 1, corresponding to the size of the vocabulary, and the output is passed through a softmax to generate a probability distribution over the vocabulary. The word with the highest probability is selected as the translated token.
The hidden state update follows the standard RNN equation:
But this raises a key question: what is x (input) in the decoder?
At timestep t = 1, x is the special token <SoS> (Start of Sequence). This is used to compute the first decoder hidden state, and consequently the first output word y1.
At timestep t = 2, the decoder uses the previous output word (or its embedding) as input.
This process continues until the model generates the <EoS> (End of Sequence) token, signaling the end of translation.
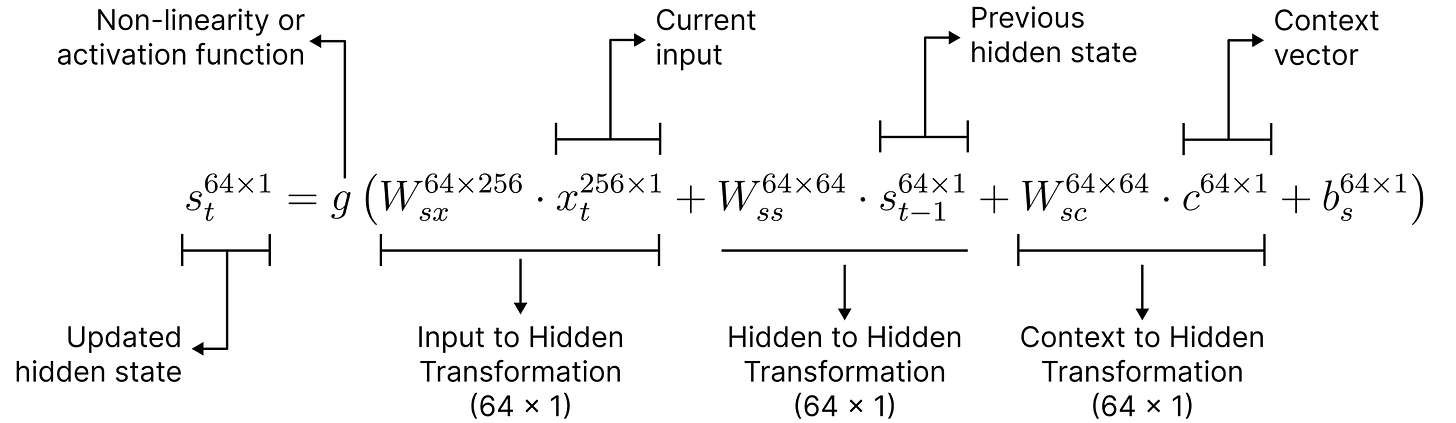
Context Vector for Decoding
In the traditional encoder-decoder architecture, the encoder produces a fixed-length context vector, say c = h3, which initializes the decoder. However, as decoding proceeds, the decoder can lose relevant context information, especially when translating longer sentences.
To mitigate this, one approach is to pass the context vector, c, as an input at every decoding timestep, not just at initialization. The updated formula becomes:
This allows the decoder to continually access the original context throughout decoding, leading to more accurate translations.
However, this raises an important limitation:
If the input sentence is very long, can a fixed-length vector truly represent all its information?
Apparently not.
What Comes Next
To address this limitation, Bahdanau et al. proposed a more effective solution: instead of using a single fixed-length vector, let the model dynamically attend to relevant parts of the input at each decoding step.
This idea led to the Bahdanau Attention mechanism, which we will explore in detail in the next post.
Stay tuned.